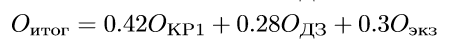Численные Методы 2021

О курсе

Этот курс численных методов похож на классическую вычислительную математику, но в то же время более практический. Студент на этой дисциплине научится владеть основными методами численного дифференцирования, интегрирования, интерполяции и аппроксимации, приближённо искать корни нелинейных уравнений и решать системы дифференциальных уравнений и многое другое. Будет рассказано о применении большинства алгоритмов в практических задачах показа медийной рекламы.

Курс читается с 2016 года.

Учебный план

Предусмотрены лекционные, семинарские занятия, 2 контрольных работы, а также курсовой проект. Все материалы курса лежат в dropbox.

Приблизительная программа лекций

Пример практической задачи: показ рекламы в сети Интернет (1 лекция, 1 семинар)

Конспект

Общая схема процесса. Отличия от традиционной рекламы. Участники процесса. Медийная и контекстная реклама. Рекламные кампании, их параметры. Описание аудитории. Пространство сегментов аудитории. Вероятностное описание посетителей. Оценка профиля посетителя Интернета. Таргет рекламной кампании. Определение вероятности попадания посетителя в целевую аудиторию. Алгоритм показа медийной рекламы с таргетированием. Упрощенная модель показа рекламы с таргетированием в Интернете. Постановка практической задачи. Необходимость применения численных методов решения.

Предмет вычислительной математики (½ лекции)

Конспект (с дифференцированием)

Специфика машинных вычислений. Элементарная теория погрешностей.

Численное дифференцирование (½ лекции, 1 семинар)

Все материалы семинара

Простейшие формулы численного дифференцирования. Оценка погрешности. Метод неопределенных коэффициентов вывода формул численного дифференцирования. Оптимальный шаг численного дифференцирования.

Приближение функций, заданных на дискретном множестве (2 лекции, 2 семинара)

Конспект (полиномы, сплайны, константа Лебега)

Конспект (многочлены Чебышёва)

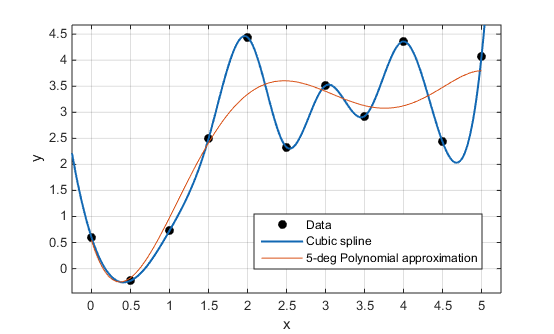
Задача алгебраической интерполяции. Существование и единственность алгебраического интерполяционного полинома. Интерполяционный полином в форме Лагранжа и в форме Ньютона. Остаточный член интерполяции. Интерполяция по чебышёвским узлам. Оценка погрешности интерполяции для функций, заданных с ошибками. Кусочно-многочленная интерполяция. Интерполяция сплайнами.

Все материалы семинаров Семинар 1 решённый данные(с шумом) данные(без шума)

Численное интегрирование (1 лекция, 1 семинар)

Конспект Семинар

Квадратурные формулы Ньютона-Котеса (прямоугольников, трапеций, Симпсона) и оценка их погрешности. Квадратурные формулы Гаусса.

Решение систем линейных алгебраических уравнений (4 лекции, 3 семинара)

Конспект 1 Конспект 2 Конспект 3 Конспект 4

доп.материалы семинаров(для чтения)

Нормы в конечномерных пространствах. Обусловленность системы линейных алгебраических уравнений. Прямые методы решения: метод Гаусса, метод Гаусса с выбором главного элемента, метод прогонки для систем специального вида. LU-разложение и его связь с методом Гаусса. Итерационные методы решения линейных систем. Метод простых итераций. Необходимое, достаточное условия сходимости метода простых итераций. Методы Якоби, Зейделя. Методы решения, основанные на минимизации функционалов. Переопределенные системы линейных алгебраических уравнений.

Методы численного решения нелинейных уравнений (1 лекция, 1 семинар)

конспект

Принцип сжимающих отображений. Метод простых итераций. Условие сходимости метода простых итераций. Метод Ньютона. Порядок сходимости и условия достижения заданной точности итерационных методов. Метод релаксации.

Численные методы решения обыкновенных дифференциальных уравнений (2 лекции, 1 семинар)

ОДУ, Краевые задачи

семинар(NBody) семинар(NBody, решённый)

Аппроксимация, устойчивость, сходимость. Теорема о связи аппроксимации, устойчивости, сходимости. Численные методы решения задачи Коши для ОДУ. Методы Рунге–Кутты и Адамса решения ОДУ. Численное решение краевых задач для ОДУ. Методы решения линейных и нелинейных краевых задач.

Применение численных методов в модели показа медийной рекламы (2 лекции, 2 семинара)

Применение численного интегрирования, табуляция результата. Использование интерполяции для вычисления функции, использование сплайнов. Численное решение системы линейных алгебраических уравнений для построения сплайна. Применение формул численного дифференцирования для аппроксимации уравнений. Численное решение задачи Коши для модели показа медийной рекламы. Имитационная модель системы показа медийной рекламы. Алгоритмы игры на аукционе RTB (Real-Time Bidding).

Курсовой проект

Курсовой проект -- домашнее задание, рассчитанное на семестр, составляющее половину оценки Одз. Проект предполагает решение какой-либо практической задачи. Студенты могут выбрать тему из предложенных здесь или предложить свою (в этом случае необходимо обсудить тему с семинаристом). Возможна работе в команде, но это тоже должно быть оговорено заранее. Ориентировочный дедлайн выбора тем по проекту будет анонсирован позже.

Домашние задания

Домашние задания нужно присылать на почту maxkaledin@gmail.com с темой "Численные методы ДЗ 1 Илья Иванов".

Все дедлайны мягкие: 1 неделю после дедлайна штраф 25%, затем ещё 25% каждую неделю. При этом максимальная оценка не падает ниже 25%.

ДЗ1 (интерполяция, сплайны, константа Лебега) Дедлайн: 25 февраля 2021, 2359

ДЗ2 (интегрирование и прямые методы для СЛАУ) Дедлайн: 19 марта 2021, 2359

ДЗ3 (задача наименьших квадратов) датасет Дедлайн: 15 мая 2021, 2359

Экзамен

Программа экзамена (4 курс, 24 марта) Программа экзамена (3 курс, 16 июня)

Правила оценивания

NEW!! ВЕДОМОСТЬ

Для обоих треков предусмотрен итоговый устный экзамен и некоторые оценочные элементы по ходу курса: контрольные и домашние работы. Их структура отличается у 3 и 4 курса, так как последние завершают учёбу в 3 модуле.

Для третьего курса (3-4 модуль)

Планируется провести две контрольных работы (КР1 и КР2), выдать домашние задания и проект (считается как более трудоёмкое домашнее задание).

Результирующая оценка по дисциплине рассчитывается по формуле

Накопленная и экзаменационная оценки округляются арифметически.

Накопленная оценка рассчитывается по формуле

где пкр - промежуточная контрольная работа, фкр - финальная контрольная работа, экз - экзамен.

Итоговая формула:

Итоговые 0.28 за ДЗ делятся между лабораторными(0.15) и проектом(0.13).

Для четвёртого курса (3 модуль)

Планируется провести одну контрольную (КР1) и выдать два домашних задания.

Накопленная оценка имеет другую формулу, экзамен будет проведён в конце третьего модуля.

Итоговая формула:

В качестве домашних заданий выступают только лабораторные.

Контакты

Записи лекций и семинаров: OneDrive YouTube

Телеграм-чат: пишите @XuMuK_MK

Максим Каледин, семинары

email: maxkaledin@gmail.com аудитория в ВШЭ: Покровский бульвар, 11, комната T926 https://www.hse.ru/staff/mkaledin

Полезные ссылки

Базовый учебник

Лобанов А.И., Петров И.Б. Лекции по вычислительной математике — М.: Интернет–Университет информационных технологий, 2006. — 522с.

Дополнительная литература

1. Рябенький В.С. Введение в вычислительную математику. — М.: Наука–Физматлит, 1994. — 335 с.; 3-е изд. — М.: Физматлит, 2008. — 288 с.
2. Косарев В.И. 12 лекций по вычислительной математике. 3-е изд. — М.: Физматкнига, 2013. — 240с.
3. Марчук Г.И. Методы вычислительной математики. — М.: Наука, 1989. — 608с. Комментарий: продвинутые методы для линейной алгебры.
4. Калиткин Н.Н. Численные методы. — М.: Наука, 1978. — 512с.
5. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы -- М.: Бином. Лаборатория знаний, 2011. -- 636с.